Question

A person lowers a bucket into a well by turning the hand crank, as the drawing illustrates. The crank handle moves with a constant tangential speed of 1.81 m/s on its circular path. The rope holding the bucket unwinds without slipping on the barrel of the crank. Find the linear speed with which the bucket moves down the well.

Answer 1

0.453 m/s

Step-by-step explanation:

Assuming the handle has diameter of 0.4 m while inner part diameter is 0.1 m then the circumference of outer part is
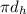`\pi d_h` where d is diameter and subscript h denote handle. By substituting 0.4 for the handle's diameter then cirxumference of outer part is
`\pi* 0.4\approx 1.256 m`

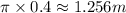
The rate of rotation will then be 1.81/1.256=1.441 rev/s

Similarly, circumference of inner part will be
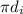`\pi d_i` where subscript i represent inner. Substituting 0.1 for inner diameter then

`\pi* 0.1\approx 0.3142 m`

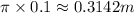
The rate of rotation found for outer handle applies for inner hence speed will be 0.3142*1.441=0.453 m/s