Question

A random sample of 1800 NAU students in Flagstaff found 1134 NAU students who love their MAT114 class. Find a 95% confidence interval for the true percent of NAU students in Flagstaff who love their MAT114 class. Express your results to the nearest hundredth of a percent. .

Answer 1

95% confidence interval for the true percent of NAU students in Flagstaff who love their MAT114 class is (60.77% , 65.23%)

Explanation:

Among 1800 NAU students, 1134 students love their class. We have to find the 95% confidence interval of students who love their class.

We will use the concept of confidence interval of population proportion for this problem.

The proportion of students who love the class = p =
`(1134)/(1800)=0.63`

Proportion of students who do not love the class = q = 1 - p = 1 - 0.63 = 0.37

Total number of students in the sample = n = 1800

Confidence Level = 95%

The z values associated with this confidence level(as seen from z table) = 1.96

The formula to calculate the confidence interval for population proportion is:

`(p-z*\sqrt{(p * q)/(n)},p+z*\sqrt{(p * q)/(n)})`

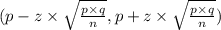
Using the values in this expression gives:

`(0.63-1.96 * \sqrt{(0.63 * 0.37)/(1800)}, 0.63+1.96 * \sqrt{(0.63 * 0.37)/(1800)})\\\\ =(0.6077,0.6523)`

Thus, 95% confidence interval for the true percent of NAU students in Flagstaff who love their MAT114 class is (0.6077 ,0.6523) or (60.77% , 65.23%