Question

Oh no! The zombie virus that began with Mr. Smith has now been passed on to students! Suppose the new virus infected 10 students all at once. Then, each newly-turned zombie infects exactly 3 other people, so that the zombie population triples every day. The formula to model this situation is P = 10(3)x

a) On what day will there be a zombie population over 2,000? Explain how you found this answer.

b) If a cure is not found and the virus continues to spread, how many new zombie will there be on day 10? Explain how you found this answer.

Answer 1

Part a) In the day 5 will be a zombie population over 2,000

Part b)
`590,490\ zombies`

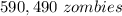
Explanation:

we know that

The equation of a exponential growth function is equal to

`P=a(1+r)^x`

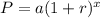
where

P is the population of zombie

x is the number of days

a is the initial value

r is the rate of change

we have

`a=10\\r=200\%=200/100=2`

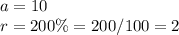
substitute

`P=10(1+2)^x`

`P=10(3)^x`

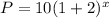
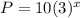
Part a) On what day will there be a zombie population over 2,000?

For P=2,000

substitute in the exponential equation

`2,000=10(3)^x`

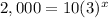
solve for x

`200=3^x`

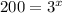
Apply log both sides

`log(200)=xlog(3)`

`x=log(200)/log(3)`

`x=4.8\ days`

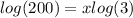
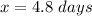
therefore

In the day 5 will be a zombie population over 2,000

Part b) If a cure is not found and the virus continues to spread, how many new zombie will there be on day 10?

For x=10 days

substitute in the equation

`P=10(3)^(10)= 590,490\ zombies`