Answer:
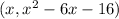 for all real numbers
for all real numbers
Explanation:
Assuming, the graph continues indefinitely.
The given function is

To find all solutions to f(x), we equate f(x) to zero.
This implies that:
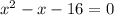
We factor to obtain:
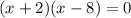
This gives us;
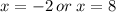
Hence the graph meets the x-axis at (-2,0) and (8,0).
These are the solutions of f(x), where the graph meets the x-axis.
But the question demands for all solutions.
Therefore
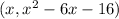 for all real numbers is the correct choice
for all real numbers is the correct choice