Question

*SAT QUESTION*

In triangle ABC, the measure of ∠B is 90°, BC=16, and AC=20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is
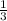
`(1)/(3)` the length of the corresponding side of triangle ABC. What is the value of sinF?

Answer 1

0.6

Step-by-step explanation:

Angle F corresponds to Angle C

sinF = sinC

AC² = AB² + BC²

20² = AB² + 16²

AB² = 400 - 256

AB² = 144

AB = 12

sinC = AB/AC

sinC = 12/20

sinF = 0.6

Answer 2

Answer and Explanation:

`Greetings!`

`Let's~answer~your~question!`

`Triangle~ ABC ~is ~a ~right~ triangle~ with ~its~ right~ angle ~at ~B. ~Therefore,~AC\\is~ the~ hypotenuse~ of~ right~ triangle~ ABC,~ and~ AB ~and ~BC ~are~ the~ legs~ of~ right~\\ triangle ~ABC.`

`According~ to~ the~ Pythagorean ~theorem,`

`AB=√(20^2-16^2)=√(400-256)=√(144)=12`

`Since ~triangle~DE`
`F~is ~similar~ to~ triangle~ ABC,~ with~ vertex ~F ~corresponding~to~ vertex~ C,~ the~ measure\\ of~angle~ \angle F~equals~ the~ measure~ of~ angle~\angle C.`

`Therefore,~ sinF=sinC. ~From ~the~ side~ lengths~ of ~triangle~ ABC,`

`sinF=(opposite ~side)/(hypotenuse) =(AB)/(AC) =(12)/(20)=(3)/(5)`

`Therfore, ~sinF=(3)/(5)~or~0.6`