Question

1 point) As reported in "Runner's World" magazine, the times of the finishers in the New York City 10 km run are normally distributed with a mean of 61 minutes and a standard deviation of 9 minutes. Let X denote finishing time for the finishers. a) The distribution of the variable X has mean 61 and standard deviation 9 . b) The distribution of the standardized variable Z has mean and standard deviation

Answer 1

(a) E (X) = 61 and SD (X) = 9

(b) E (Z) = 0 and SD (Z) = 1

Explanation:

The time of the finishers in the New York City 10 km run are normally distributed with a mean,μ = 61 minutes and a standard deviation, σ = 9 minutes.

(a)

The random variable X is defined as the finishing time for the finishers.

Then the expected value of X is:

E (X) = 61 minutes

The variance of the random variable X is:

V (X) = (9 minutes)²

Then the standard deviation of the random variable X is:

SD (X) = 9 minutes

(b)

The random variable Z is the standardized form of the random variable X.

It is defined as:
`Z=(X-\mu)/(\sigma)`

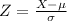
Compute the expected value of Z as follows:

`E(Z)=E[(X-\mu)/(\sigma)]\\=(E(X)-\mu)/(\sigma)\\=(61-61)/(9)\\=0`

The mean of Z is 0.

Compute the variance of Z as follows:

`V(Z)=V[(X-\mu)/(\sigma)]\\=(V(X)+V(\mu))/(\sigma^(2))\\=(V(X))/(\sigma^(2))\\=(9^(2))/(9^(2))\\=1`

The variance of Z is 1.

So the standard deviation is 1.