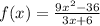Question

Which graph represents the function of 9x^2 - 36 over 3x + 6

Answer 1

the first graph

Explanation:

Answer 2

`f(x)=(9x^2-36)/(3x+6)` If this is what you mean,

Notice clearly, we can factor 9x^2-36 out, same with 3x+6

`f(x)=(9(x^2-4))/(3(x+2))\\f(x)=(9(x+2)(x-2))/(3(x+2))\\f(x)=(9(x-2))/(3)\\\\f(x)=(3(x-2))/(1)\\f(x)=3(x-2)\\f(x)=3x-6`

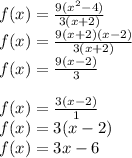
From x^2-4, use the Difference of Two Squares,
`x^2-y^2=(x+y)(x-y)`

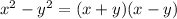
To find the x-intercept, y or f(x) = 0

`0=3x-6\\6=3x\\x=2`

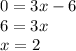
Now we know the x-intercept. To find the y-intercept, x = 0 therefore,

`f(0)=3x-6\\f(0)=3(0)-6\\f(0)=-6`

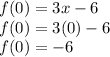
So point or dot at x = 2 and y = -6 then draw the line. It should be like the graph shown below (Image.)