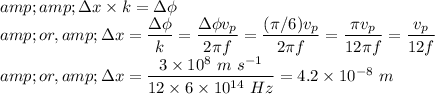Answer:
The shortest distance covered by the wave between the given points is
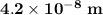 .
.
Step-by-step explanation:
The Phase velocity (
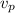 ) of any wave can be written as
) of any wave can be written as
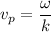
where '
 ' is the angular velocity and '
' is the angular velocity and '
 ' is the wave number.
' is the wave number.
Also, if '
 ' is the frequency of the wave, then
' is the frequency of the wave, then
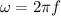
Given,
 ,
,
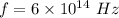 and the phase difference between two points is
and the phase difference between two points is
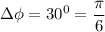 .
.
If the wave travels by the shortest distance of
 between these points, then we can write
between these points, then we can write