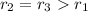Complete Question
The complete question is shown on the first uploaded image
Answer:
a
The Ranking of the curve according to their speed would be equal Rank because

b
The first frequency would have a higher rank compared to the other two which will have the same ranking when ranked with respect to their angular velocities because
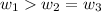
c
The ranking of the second third frequency would be the same but their ranking would be greater than that of the first frequency because
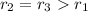
Step-by-step explanation:
Mathematically Frequency can be represented as
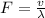
Where
 is the wavelength and v is the velocity
is the wavelength and v is the velocity
Now looking at the diagram we see that
For the first frequency we have
Let the wavelength be
 , and the frequency
, and the frequency
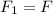
For the second frequency
Let the wavelength be
 , and the frequency
, and the frequency
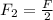
For the third frequency
Let the wavelength be
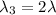 , and the frequency
, and the frequency
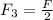
To obtain v for each of the frequency we make v the subject in the equation above for each frequency
So,
For the first frequency we have
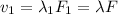
For the second frequency
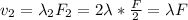
For the third frequency
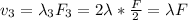
Hence
The Ranking of the curve according to their speed would be equal Rank because

Mathematically angular speed can be represented as
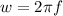
For the first frequency we have
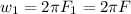
For the second frequency
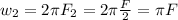
For the third frequency

Hence
The first frequency would have a higher rank compared to the other two which will have the same ranking when ranked with respect to their angular velocities because
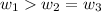
Mathematically the relationship between the angular velocity and the linear velocity can be represented as
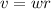
=>

Since the linear velocity is constant we have that
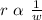
This means that r varies inversely to the angular velocity ,What this means for ranking due to the radius is that the ranking of the second third frequency would be the same but their ranking would be greater than that of the first frequency because