Question

A small foundry agrees to pay $220,000 two years from now to a supplier for a given amount of coking coal. The foundry plans to deposit a fixed amount in a bank account every three months, starting three months from now, so that at the end of two years the account holds $220,000.

If the account pays 12.5% APR compounded monthly, how much must be deposited every three months?


A) $24,602

B) $27,063

C) $29,523

D) $31,983

Answer 1

A) $24,602

Step-by-step explanation:

We can solve this question by finding the periodic deposits needed by using the formula:

`FV=PMT*((1+i)^n-1)/(i)`

where:

FV= future value = $220,000

PMT = periodic deposits required = ???

i = effective interest rate per period = 0.0331

n= number of deposits = 8

However, since the interest is compounded monthly, let's also calculate the effective interest rate

Effective interest rate =
`(1+(r)/(m)) ^m-1`

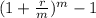
where; r = 12.5% = 0.125

`(1+(0.125)/(12))^(12) -1`

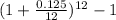
= 0.1324

Interest rate per period =
`(0.1324)/(4)`

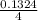
= 0.0331

Then;

`220,000=PMT*((1+0.033)^8-1)/(0.033)`

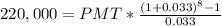
220,000 = PMT × 8.986

PMT =
`(220,000)/(8.986)`

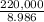
PMT = $ 24,482.5

Since A) $24,602 is closer to $ 24,482.5

Therefore, $ $24,602 must be deposited every three months