Question

A specimen of aluminum having a rectangular cross-section of 10 mm x 12.7 mm is pulled in tension with 35,500 N of force, producing only elastic deformation. Calculate the resulting strain.

Answer 1

Step-by-step explanation:

The given data is as follows.

Cross-section area of the rectangular is as follows.

Area =
`10 mm * 12.7 mm`

=
`127 * 10^(-6) m^(2)`

=
`1.27 * 10^(-4) m^(2)`

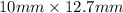
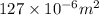
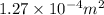
Tension applied on the specimen is 35,500 N

Now, formula to calculate the modulus of elasticity for a material of aluminium is as follows.

E = 70 GPa

=
`70 * 10^(9) Pa`

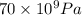
or, =
`70 * 10^(9) N/m^(2)`

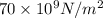
Now, stress on the specimen is as follows.

`\sigma = (P)/(A)`

=
`(35000)/(1.27 * 10^(-4))`

=
`275.59 * 10^(6) N/m^(2)`

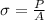
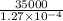
According to Hook's law, we will calculate the resulting stain as follows.

`\sigma = E \epsilon`

`\epsilon = (\sigma)/(E)`

=
`(275.59 * 10^(6))/(70 * 10^(9))`

=
`3.937 * 10^(-3) mm/mm`

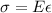
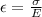
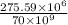
Thus, we can conclude that the resulting strain is
`3.937 * 10^(-3) mm/mm`.