Question

A manufacturing company produces valves of different sizes and shapes. One valve plate is supposed to have a tensile strength of 5 lbs/mm and is known to have a standard deviation of 0.28 lbs/mm. The company tests a randomly selected sample of 32 valve plates and finds the plates have an average tensile strength of 4.9289 lbs/mm

Answer 1

a) Null hypothesis:
`\mu = 5`

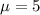
Alternative hypothesis:
`\mu \\eq 5`

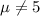
b) The significance level is
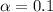`\alpha= 0.1`, and
`\alpha/2 = 0.05` so then the critical values are for this case:

`z_(crit)= \pm 1.64`

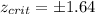
c) t-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".

We can replace in formula (1) the info given like this:

`t=(4.9289-5)/((0.28)/(√(32)))=-1.436`

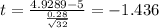
d) Since the calculated value is lower than the critical value we don't have enough evidence to reject the null hypothesis at a significance level of 0.1

e) Since is a bilateral test the p value would be:

`p_v =2*P(z<-1.436)=0.151`

Explanation:

We assume the following questions:

a) What is the appropriate null and alternate hypothesis to determine if the average tensile strength of the valve plate is different than 5 lbs/mm?

We need to conduct a hypothesis in order to check if the mean is equal to 5 or no, the system of hypothesis would be:

Null hypothesis:
`\mu = 5`

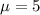
Alternative hypothesis:
`\mu \\eq 5`

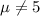
b) Using \alpha= 0.10, what are the critical values for the hypothesis test?

For this case since the population deviation is known
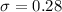`\sigma = 0.28`, we can use the normal standard distribution for the critical values.

The significance level is
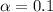`\alpha= 0.1`, and
`\alpha/2 = 0.05` so then the critical values are for this case:

`z_(crit)= \pm 1.64`

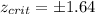
c) What is the test statistic for the hypothesis test?

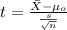`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

t-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".

We can replace in formula (1) the info given like this:

`t=(4.9289-5)/((0.28)/(√(32)))=-1.436`

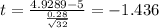
d) Draw a conclusion for the hypothesis test. Make sure you state your conclusion in the context of the problem.

Since the calculated value is lower than the critical value we don't have enough evidence to reject the null hypothesis at a significance level of 0.1

e) Calculate the p-value for the hypothesis test.

Since is a bilateral test the p value would be:

`p_v =2*P(z<-1.436)=0.151`