Question

A random sample of 15 observations from the first population revealed a sample mean of 350 and a sample standard deviation of 12. A random sample of 17 observations from the second population revealed a sample mean of 342 and a sample standard deviation of 15. At the .05 significance level, what is the p-value for testing variances for a one-tail test?

Answer 1

Explanation:

Hello!

You have two random samples obtained from two different normal populations.

Sample 1

n₁= 15

X[bar]₁= 350

S₁= 12

Sample 2

n₂= 17

X[bar]₂= 342

S₂= 15

At α: 0.05 you need to obtain the p-value for testing variances for a one tailed test.

If the statistic hypotheses are:

H₀: σ₁² ≥ σ₂²

H₁: σ₁² < σ₂²

The statistic to test the variances ratio is the Stenecor's-F test.
`F_(H_0)=((S^2_1)/(Sigma^2_1)) * ((S^2_2)/(Sigma^2_2) )`~
`F_(n_1-1;n_2-1)`

`F_(H_0)= ((12)^2)/((15)^2) * 1= 0.64`

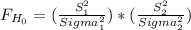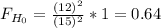
The p-value is:

P(
`F_(14;16)`≤0.64)= 0.02

I hope it helps!