Question

Two satellites are in circular orbits around the earth. The orbit for satellite A is at a height of 403 km above the earth’s surface, while that for satellite B is at a height of 732 km. Find the orbital speed for (a) satellite A and (b) satellite B.

Answer 1

`v_A=7667m/s\\\\v_B=7487m/s`

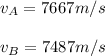
Step-by-step explanation:

The gravitational force exerted on the satellites is given by the Newton's Law of Universal Gravitation:

`F_g=(GMm)/(R^(2) )`

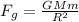
Where M is the mass of the earth, m is the mass of a satellite, R the radius of its orbit and G is the gravitational constant.

Also, we know that the centripetal force of an object describing a circular motion is given by:

`F_c=m(v^(2))/(R)`

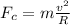
Where m is the mass of the object, v is its speed and R is its distance to the center of the circle.

Then, since the gravitational force is the centripetal force in this case, we can equalize the two expressions and solve for v:

`(GMm)/(R^2)=m(v^2)/(R)\\ \\\implies v=\sqrt{(GM)/(R)}`

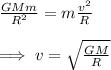
Finally, we plug in the values for G (6.67*10^-11Nm^2/kg^2), M (5.97*10^24kg) and R for each satellite. Take in account that R is the radius of the orbit, not the distance to the planet's surface. So
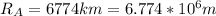`R_A=6774km=6.774*10^6m` and
`R_B=7103km=7.103*10^6m` (Since
`R_(earth)=6371km`). Then, we get:

`v_A=\sqrt{((6.67*10^(-11)Nm^2/kg^2)(5.97*10^(24)kg))/(6.774*10^6m) }=7667m/s\\\\v_B=\sqrt{((6.67*10^(-11)Nm^2/kg^2)(5.97*10^(24)kg))/(7.103*10^6m) }=7487m/s`

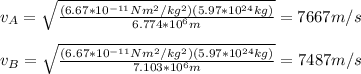
In words, the orbital speed for satellite A is 7667m/s (a) and for satellite B is 7487m/s (b).