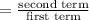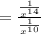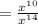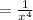Question

Find the common ratio of the geometric sequence.


`(1)/(x^(10)), (1)/(x^(14)), (1)/(x^(18)), (1)/(x^(22)), .......`

Answer 1

The common ratio is
`(1)/(x^4)`

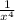
Explanation:

Geometric sequence:A geometric sequence is a sequence in which the ratio of any term to the preceding term of that term is always constant.

Common ratio: The ratio of any term to the preceding term of that term.

The
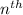`n^(th)` term of a geometric sequence is represented by
`a_n=ar^(n-1)`.

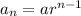The
`1^(st)` term of the sequence = a.

The sum of first n term is

`S_n=(a(1-r^n))/(1-r)`

The common ratio = r.

Given geometric sequence,

`(1)/(x^(10))` ,
`(1)/(x^(14))`,
`(1)/(x^(18))`,
`(1)/(x^(22))` ........

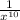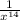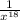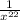The common ratio is

`=\frac{\textrm{second term}}{\textrm{first term}}`

`=((1)/(x^(14)))/((1)/(x^(10)))`

`=(x^(10))/(x^(14))`

`=(1)/(x^4)`