Question

Which polynomial function has a leading coefficient of 1, roots -2 and 7 with multiplicity 1, and root 5 with multiplicity 2?

A) f(x) = 2(x + 7)(x + 5)(x - 2)
B) f(x) = 2(x - 7)(x - 5)(x + 2)
C) f(x) = (x + 7)(x + 5)(x + 5)(x - 2)
D) f(x) = (x - 7)(x - 5)(x - 5)(x + 2)

Answer 1

D

Step-by-step explanation:

EDGE2020

Answer 2

Option D:
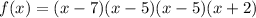`f(x) = (x - 7)(x - 5)(x - 5)(x + 2)` is the polynomial

Step-by-step explanation:

Given that we need to determine the polynomial that has a leading coefficient of 1, roots -2 and 7 with multiplicity 1 and root 5 with multiplicity 2

Option A:
`f(x) = 2(x + 7)(x + 5)(x - 2)`

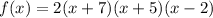
The polynomial has roots -7, -5 and 2 with multiplicity 1.

Hence, Option A is not the correct answer.

Option B:
`f(x) = 2(x - 7)(x - 5)(x + 2)`

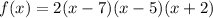
The polynomial has roots 7,5 and -2 with multiplicity 1.

Hence, Option B is not the correct answer.

Option C:
`f(x) = (x + 7)(x + 5)(x + 5)(x - 2)`

The polynomial has roots 2 and -7 with multiplicity 1 and root -5 with multiplicity 2.

Hence, Option C is not the correct answer.

Option D:
`f(x) = (x - 7)(x - 5)(x - 5)(x + 2)`

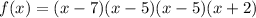
The polynomial has roots -2 and 7 with multiplicity 1 and root 5 with multiplicity 2.

Hence, Option D is the correct answer.