Question

In a manufacturing process, a random sample of 9 bolts has a mean length of 3 inches with a variance of .09. What is the 90 percent confidence interval for the true mean length of the bolt

Answer 1

Question:

In a manufacturing process, a random sample of 9 bolts has a mean length of 3 inches with a variance of .09. What is the 90 percent confidence interval for the true mean length of the bolt:

A. 2.8355 to 3.

B. 2.5065 to 3.

C. 2.4420 to 3.

D. 2.8140 to 3.

E. 2.9442 to 3

Answer:

The answer is D

Step-by-step explanation:

Step 1

Subtract 1 from your sample size 9 – 1 = 8. This gives you degrees of freedom, which you’ll need in step 3.

Step 2

Subtract the confidence level from 1, then divide by two.

(1 –0.90) / 2 = 0.05

Step 3

Look up your answers to step 1 and 2 in the t-distribution table. For 8 degrees of freedom (df) and α = 0.05, my result is 1.860

Step 4

Get your Standard deviation.

Standard deviation is simply the root of your variance. That is

SD =
`√(Variance)`

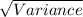
Thus SD =
`√(0.09)`

SD = 0.3

Step 5

Calculate Standard Error

Do this by Dividing your sample standard deviation by the square root of your sample size.

SE=
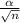`(\alpha )/(√(n) )` Where n is sample size and
`\alpha` = standard deviation

SE = 0.3/
`√(9)`

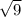
SE = 0.3/3

SE = 0.1

Step 6

Multiply T-Value by Standard Error

= 1.860 x 0.1

= 0.186

Step 7

To get the upper value and lower values of Confidence Interval

We add and take the mean from the figure obtained in step 6.

We subtract the mean to the above figure

= 3-0.186

= 2.814 (Lower Limit of Confidence Interval)

Here we add

3 + 0.186

= 3.186 (Upper Limit of Confidence Interval) or Approximately 3.

Cheers!