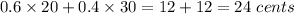Question

It costs 20 cents to receive a photo and 30 cents to send a photo from a cellphone. C is the cost of one photo (either sent or received). The probability of receiving a photo is 0.6. The probability sending a photo is 0.4. (a) Find PC(c), the PMF of C. (b) What is E[C], the expected value of C

Answer 1

(a) PC(C)=
`\left \{ {{0.6 \ \ \ \ x=20} \atop 0.4 \ \ \ \ {x=30}} \right. \\\ 0 \ \ \ \ \ \ \ else`

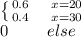
(b) E[C] = 24 cents

Explanation:

Given:

Cost to receive a photo = 20 cents

Cost to send a photo = 30 cents

Probability of receiving a photo = 0.6

Probability of sending a photo = 0.4

We need to find

(a) PC(c)

(b) E[C]

Solution:

(a)

PC(C)=
`\left \{ {{0.6 \ \ \ \ c=20} \atop 0.4 \ \ \ \ {c=30}} \right. \\\ 0 \ \ \ \ \ \ \ else`

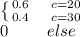
(b)

Expected value can be calculated by multiplying probability with cost.

E[C] = Probability × cost

E[C] =
`0.6*20 +0.4 * 30 = 12 + 12 = 24\ cents`