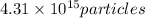Question

Particles with a charge of +5e are incident on a target. If the beam of particles carries a current of 138 µA, how many particles strike the target in a period of 25.0 s? particles

Answer 1

`4.31*10^(15)particles`

Step-by-step explanation:

Current (I) is the flow of charge (Q) per unit of time (t). The ampere unit is defined as the amount of charge that flows in one second.

`Current=I=(Q)/(t)`

`1\text{ }ampere=1(coulomb)/(second)`

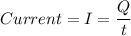
You have the current, 138 µA, and the time, 25.0s, thus you can calculate the charge:

`Q=I* t=138\mu A* (10^(-6)A)/(\mu A)* 25.0s=0.00345C`

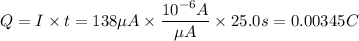
Now calculate the number of particles with a charge of +5eV that have a charge of 0.00345C

The charge of one electron is
`1.602* 10^(-19)C`

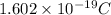
Then, a positve charge equivalent to the magnitude of the charge of 5 electrons (one particle) is:

`5* 1.602* 10^(-19)C=8.010* 10^(-19)C`

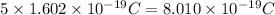
Divide the total charge by the charge of a particle:

`(0.00345C)/(8.010* 10^(-19)C)=4.3071* 10^(15)`

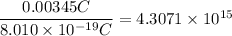
Rounding to 3 significant figures that is
`4.31* 10^(15)particles`