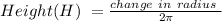Answer:
The Height is H = 70.02 m
Step-by-step explanation:
We are given that the
Initial length is =
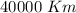 =
=
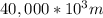
from what we are told in the question the circumference of the circle is =
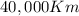
This means that the Radius would be :
Let C denote the circumference
So
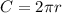
=>
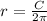
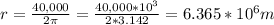
We are told that 1-meter bar of steel that increases its temperature by 1 degree C will expand
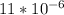 meters
meters
Hence
The final length would be
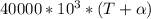
Where T is the change in temperature
 is the Coefficient of linear expansion for steel
is the Coefficient of linear expansion for steel
let
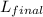 denote the final length
denote the final length
So
![L_(final) =40000*10^(6) *[1+ 11*10^(-6)]](https://img.qammunity.org/2021/formulas/physics/college/55zmz2x0myya6jiucrpy5k9sbi4nnsm2lr.png)
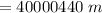
Now the Height is mathematically represented as