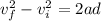Question

The drag on a pitched baseball can be surprisingly large. Suppose a 145 g baseball with a diameter of 7.4 cm has an initial speed of 40.2 m/s (90 mph). Drag coefficient for a pitched baseball equals 0.35.

Part A: What is the magnitude of the ball's acceleration due to the drag force?


Part B: If the ball had this same acceleration during its entire 18.4 m trajectory, what would its final speed be?

Answer 1

Part A)

Acceleration of the ball is 10.1 m/s/s

Part B)

the final speed of the ball is given as

`v_f = 35.3 m/s`

Step-by-step explanation:

Part a)

As we know that drag force is given as

`F = (C_d \rho A v^2)/(2)`

`C_d = 0.35`

`A = (\pi d^2)/(4)`

`A = (\pi(0.074)^2)/(4)`

`A = 4.3 * 10^(-3) m^2`

`v = 40.2 m/s`

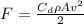
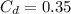
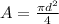
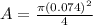
so we have

`F = (0.35* 1.2 (4.3 * 10^(-3))(40.2)^2)/(2)`

`F = 1.46 N`

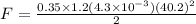
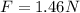
So acceleration of the ball is

`a = (F)/(m)`

`a = (1.46)/(0.145)`

`a = 10.1 m/s^2`

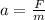
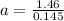
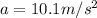
Part B)

As per kinematics we know that

`v_f^2 - v_i^2 = 2 a d`

`v_f^2 - 40.2^2 = 2(-10.1)(18.4)`

`v_f = 35.3 m/s`