Question

11. Given the kite shown below with TW=5 cm, TX = 12 cm and TZ = 4 cm.

W
Which of the following is closest, in cm, to the perimeter of the kite?
39
42
160
240

Answer 1

Answer: 39 cm

Explanation:

Let's asume the kite is the shown in the attached figure, where TW=5 cm, TX=12 cm and TZ=4 cm.

Well, firstly we have to find the value of the unknown sides to calculate the perimeter, asuming both the top and the bottom part of the kite are isosceles triangles.

For the top part, we can use the Pithagoream Theorem for the triangle TWZ, where TZ=4 cm and TW=5 cm. Hence, we have to find WZ:

`TW^(2)=TZ^(2)+WZ^(2)`

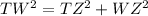
Isolating
`WZ`:

`WZ=\sqrt{TW^(2)-TZ^(2)}=\sqrt{(5 cm)^(2)-(4 cm)^(2)}`

`WZ=3 cm`

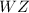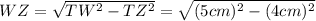
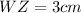
For the bottom part , we can use again the Pithagoream Theorem for the triangle WZX, where WZ=3 cm, ZX=8 cm. Hence, we have to find WX:

`WX^(2)=WZ^(2)+ZX^(2)`

`WX=\sqrt{WZ^(2)+ZX^(2)}=\sqrt{(3 cm)^(2)+(8 cm)^(2)}`

`WX=8.54 cm`

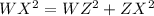
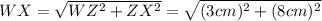
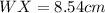
Now that we have all the sides, we can calculate the perimeter:

`5cm + 5cm +8.54 cm + 8.54 cm=27.08 cm`

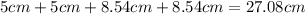
And the option that is near this value is 39 cm.