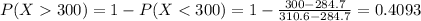Question

QUESTION 1 The driving distance for the top 100 golfers on the PGA tour is between 284.7 and 310.6 yards.Assume that the driving distance for these golfers is uniformly distributed over this interv gal.What is the probability the driving distance for one of these golfers is more than 300 yards?

Answer 1

`P(X>300)`

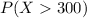
And we can find this probability with the complement rule:

`P(X>300)= 1-P(X<300) = 1-(300-284.7)/(310.6-284.7) =0.4093`

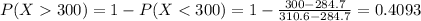
Explanation:

For this case we define the random variable X ="driving distance for the top 100 golfers on the PGA tour" and we know that:

`X \sim Unif (a=284.7, b=310.6)`

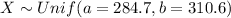
And for this case the probability density function is given by:

`f(x) =(1)/(310.6 -284.7) =0.0386 , 284.7 \leq X \leq 310.6`

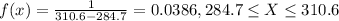
And the cumulative distribution function is given by:

`F(x) =(x-284.7)/(310.6-284.7) , 284.7 \leq X \leq 310.6`

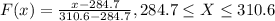
And we want to find this probability:

`P(X>300)`

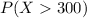
And we can find this probability with the complement rule:

`P(X>300)= 1-P(X<300) = 1-(300-284.7)/(310.6-284.7) =0.4093`