Answer: 86.2 g of
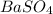 will be produced from the given masses of both reactants.
will be produced from the given masses of both reactants.
Step-by-step explanation:
To calculate the moles, we use the equation:
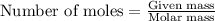
a) moles of
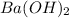
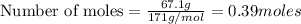
b) moles of
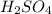
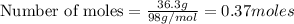
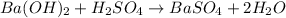
According to stoichiometry :
1 moles of
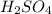 require 1 mole of
require 1 mole of
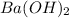
Thus 0.37 moles of
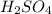 require=
require=
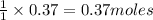 of
of
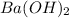
Thus
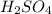 is the limiting reagent as it limits the formation of product.
is the limiting reagent as it limits the formation of product.
As 1 mole of
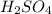 give = 1 mole of [texBaSO_4[/tex]
give = 1 mole of [texBaSO_4[/tex]
Thus 0.37 moles of
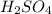 give =
give =
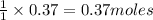 of
of
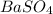
Mass of

Thus 86.2 g of
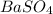 will be produced from the given masses of both reactants.
will be produced from the given masses of both reactants.