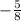Answer:
The equation of the axis of symmetry is x =
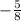
The coordinates of the vertex are (
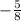 ,
,
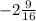 ) ⇒ 2nd answer
) ⇒ 2nd answer
Explanation:
The quadratic function y = ax² + bx + c is represented graphically by a parabola which has a minimum/maximum vertex (h , k), where
- h =
 and k is value y at x = h
and k is value y at x = h - The axis of symmetry of the parabola is a vertical line passes through the vertex point and its equation is x = h
- The minimum/maximum value of the function is (h , k)
∵ y = 4x² + 5x - 1
∵ The form of the quadratic function is y = ax² + bx + c
∴ a = 4 , b = 5 , c = -1
∵ The coordinates of the vertex points are (h , k)
∵ h =

∴ h =

- To find k substitute x in the function by
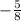
∵ k = 4 (
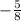 )² + 5(
)² + 5(
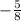 ) - 1
) - 1
∴ k = 4 (
 ) + (
) + (
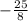 ) - 1
) - 1
∴ k =
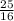 -
-
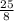 - 1
- 1
∴ k =
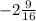
∴ The coordinates of the vertex are (
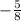 ,
,
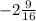 )
)
∵ The equation of the axis of symmetry is x = h
∵ h =
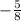
∴ The equation of the axis of symmetry is x =