The solutions of the equation are
 and
and

Step-by-step explanation:
Given that the equation is
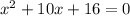
We need to determine the solutions of the equation.
The solution can be determined by factoring the equation.
Thus, we have,
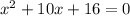
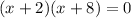
Simplifying, we get,
 and
and

Thus, the solutions of the equation are
 and
and

Now, we shall write the equation in standard form.
The equation in standard form is given by
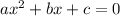
Hence, the equation
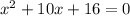 is in standard form.
is in standard form.