Question

A new shopping mall is gaining in popularity. Every day since it opened, the number of shoppers is 20%, percent more than the number of shoppers the day before. The total number of shoppers over the first 4 days is 671.

How many shoppers were at the mall on the first day?
Round your final answer to the nearest integer.

Answer 1

There were 125 shoppers on the first day.

Explanation:

Let us call the number of shoppers on the first day
`a_1`, then on the nth day the number of shoppers
`a_n` is

`a_n = a_1 (1.20)^(n-1)`

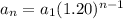
which is a geometric series whose sum to the nth term is

`$\sum_(n=0)^(n-1) a_1(r^n) = a_1(1-r^n)/(1-r) $`

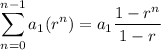
Now, we know that the total number of shoppers over the first 4 days is 671; therefore,

`a_1(1-r^n)/(1-r^n) = 671 $`

`a_1(1-(1.2)^4)/(1-(1.2)) = 671 $`

`a_1(5.368) = 671 $`

`a_1 = (671)/(5.368)`

`\boxed{a_1 = 125 \;people. }`

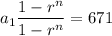
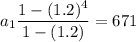
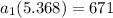
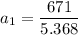
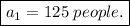
Thus, there were 125 shoppers on the first day.