Question

In one region, the September energy consumption levels for single-family homes are found to be normally distributed with a mean of 1050 kWh and a standard deviation of 218 kWh. For a randomly selected home, find the probability that the September energy consumption level is between 1100 kWh and 1225 kWh.

Answer 1

The probability that the September energy consumption level is between 1100 kWh and 1225 kWh is 0.1972

Step-by-step explanation:

The energy consumption level for a single family in September is normally distributed, therefore to solve this problem, we are going to use the z score. Z score shows the relationship of a group of values to the mean measured in terms of standard deviation from the mean.

From the question, the mean(m) = 1050 kWh

Standard deviation(s) = 218 kWh

The formula for the z score(z) where x is the raw score is given as:

z =
`(x-m)/(s)`

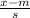
Therefore to get the probability that the September energy consumption level is between 1100 kWh and 1225 kWh, we calculate the z score for 1100 kWh and then for 1225 kWh.

For 1100 kWh,
`z=(x-m)/(s) = (1100-1050)/(218) = 0.23`

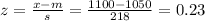
For 1225 kWh,
`z=(x-m)/(s) = (1225-1050)/(218) =0.80`

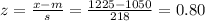
The probability that the September energy consumption level is between 1100 kWh and 1225 kWh is given by:

P(1100<x<1225) = P(0.23<z<0.8) = 0.78814 - 0.59095 = 0.1972

The probability that the September energy consumption level is between 1100 kWh and 1225 kWh is 0.1972