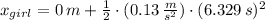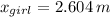Answer:
a)
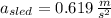 , b)
, b)
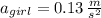 , c)
, c)
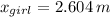
Step-by-step explanation:
a) The acceleration magnitude for the sled is:
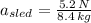
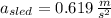
b) The acceleration magnitude for the girl is:
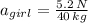
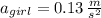
c) The position equations for the girl and sled are, respectively:
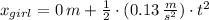
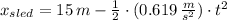
It is needed to know in which time the girl and sled meet each other. That is:
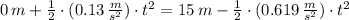
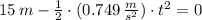
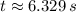
The final position in comparison with the initial position of the girl is: