Question

For about $1 billion in new space shuttle expenditures, NASA has proposed to install new heat pumps, power heads, heat exchangers, and combustion chambers. These will lower the mission catastrophe probability to 1 in 120. Assume that these changes are made. Calculate the probability of one or more catastrophes in the next:

(1) two missions
probablility=
(2) five missions
probablility=
(3) ten missions
probablility=
(4) fifty missions
probablility=

Answer 1

The probability of one or more catastrophes in:

(1) Two mission is 0.0166.

(2) Five mission is 0.0410.

(3) Ten mission is 0.0803.

(4) Fifty mission is 0.3419.

Explanation:

Let X = number of catastrophes in the missions.

The probability of a catastrophe in a mission is, P (X) =
`p=(1)/(120)`.

The random variable X follows a Binomial distribution with parameters n and p.

The probability mass function of X is:

`P(X=x)={n\choose x}(1)/(120)^(x)(1-(1)/(120))^(n-x);\x=0,1,2,3...`

In this case we need to compute the probability of 1 or more than 1 catastrophes in n missions.

Then the value of P (X ≥ 1) is:

P (X ≥ 1) = 1 - P (X < 1)

= 1 - P (X = 0)

`=1-{n\choose 0}(1)/(120)^(0)(1-(1)/(120))^(n-0)\\=1-(1*1*(1-(1)/(120))^(n-0))\\=1-(1-(1)/(120))^(n-0)`

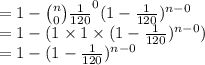
(1)

Compute the compute the probability of 1 or more than 1 catastrophes in 2 missions as follows:

`P(X\geq 1)=1-(1-(1)/(120))^(2-0)=1-0.9834=0.0166`

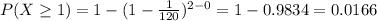
(2)

Compute the compute the probability of 1 or more than 1 catastrophes in 5 missions as follows:

`P(X\geq 1)=1-(1-(1)/(120))^(5-0)=1-0.9590=0.0410`

(3)

Compute the compute the probability of 1 or more than 1 catastrophes in 10 missions as follows:

`P(X\geq 1)=1-(1-(1)/(120))^(10-0)=1-0.9197=0.0803`

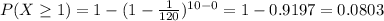
(4)

Compute the compute the probability of 1 or more than 1 catastrophes in 50 missions as follows:

`P(X\geq 1)=1-(1-(1)/(120))^(50-0)=1-0.6581=0.3419`