Question

The heat of vaporization ΔΗν of tetrahydrofuran (C4H80) is 32.0 kJ/mol. Calculate the change in entropy AS when 8.2 g of tetrahydrofuran boils at 66.0 °C Be sure your answer contains a unit symbol and the correct number of significant digits.

Answer 1

Answer: The entropy change of the tetrahydrofuran is 70.8 J/K

Step-by-step explanation:

To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

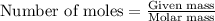
Given mass of tetrahydrofuran = 8.2 g

Molar mass of tetrahydrofuran = 72 g/mol

Putting values in above equation, we get:

`\text{Moles of tetrahydrofuran}=(8.2g)/(72g/mol)=0.114mol`

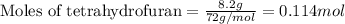
To calculate the entropy change for different phase at same temperature, we use the equation:

`\Delta S=n* (\Delta H_(vap))/(T)`

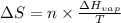
where,

`\Delta S` = Entropy change = ?

n = moles of tetrahydrofuran = 0.114 moles

`\Delta H_(vap)` = enthalpy of vaporization = 32.0 kJ/mol = 32000 J/mol (Conversion factor: 1 kJ = 1000 J)

T = temperature of the system =
`66.0^oC=[66+273]K=339K`

Putting values in above equation, we get:

`\Delta S=(0.114mol* 32000J/mol)/(339K)\\\\\Delta S=10.8J/K`

Hence, the entropy change of the tetrahydrofuran is 70.8 J/K