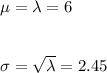Answer:
a) 0.138
b) 0.938
c) 0.544
d) 6
e) 2.45
Explanation:
Let X represent the number of tracks counted in 1 cm^2 of surface area.
The estimated average is 6 tracks per cm^2. This is the parameter λ of the Poisson distribution.
The expression for the Poisson distribution is

Then
a) x=7
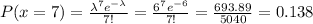
b) x≥3

c) 2<x<7

d) and e)