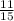Question

A jar contains 8 red marbles numbered 1 to 8 and 7 blue marbles numbered 1 to 7. A marble is drawn at random from the jar. Find the probability that the marble is blue or even-numbered.

Answer 1

Therefore the probability that the marble is blue or even numbered is
`(11)/(15)`

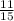
Explanation:

Probability: The ratio of favorable outcomes to the total outcomes.

It is denoted by P.

`Probability= \frac{\textrm{favorable outcomes}}{\textrm{Total outcomes}}`

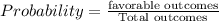
Given that a jar contains 8 red marbles and 7 blue marbles.

Total number of marbles = (8+7) = 15

Let A = Event of getting a blue marble

B= Event of getting of even marble.

Even number blue marbles are 2, 4,6

Even number red marbles are 2, 4,6,8

The number of even marbles are =(3+4)=7

The probability of getting a blue marble is P(A)

`=\frac{\textrm{Total number of blue marbles}}{\textrm{Total number of blue marbles}}`

`=(7)/(15)`

The probability of getting a even marble is P(B)

`=\frac{\textrm{The number of even number marbles}}{\textrm{Total number of marbles}}`

`=(7)/(15)`

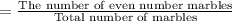
The probability of getting a even numbered blue marble P(A∩B)

`=(3)/(16)`

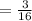
P(blue marble or even- numbered)

=P(A∪B)

=P(A)+P(B)-P(A∩B)

`=(7)/(15) +(7)/(15)-(3)/(15)`

`=(11)/(15)`

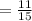
Therefore the probability that the marble is blue or even numbered is
`(11)/(15)`