Question

Find the inverse of:

(x-7)/x with steps

Answer 1

So , Inverse of
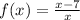`f(x) = (x-7)/(x)` is
`x = (-7)/(y-1)`.

Explanation:

An inverse function is a function that "reverses" another function: if the function f applied to an input x gives a result of y, then applying its inverse function g to y gives the result x, and vice versa, i.e., f(x) = y if and only if g(y) = x. As an example, consider the real-valued function of a real variable given by f(x) = 5x − 7. In functional notation this inverse function would be given by,

`{\displaystyle g(y)={\frac {y+7}{5}}}`

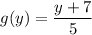
With y = 5x − 7 we have that f(x) = y and g(y) = x. Here we have
`f(x) = (x-7)/(x)`

`f(x) = (x-7)/(x)`

⇒
`f(x) = (x-7)/(x)`

⇒
`f(x) =1- (7)/(x)`

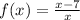
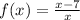
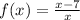
Let f(x) = y:

⇒
`f(x) =1- (7)/(x)`

⇒
`y = 1 - (7)/(x)`

⇒
`y -1 = (-7)/(x)`

⇒
`x = (-7)/(y-1)`

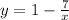
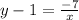
So , Inverse of
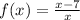`f(x) = (x-7)/(x)` is
`x = (-7)/(y-1)`.