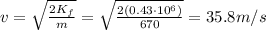a)
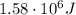
b)
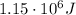
c)
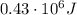
d) 35.8 m/s
Step-by-step explanation:
a)
The gravitational potential energy of an object is the energy possessed by the object due to its location with respect to the ground.
It is given by:
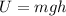
where
m is the mass of the object
g is the acceleration due to gravity
h is the height of the object, relative to a reference level
Here, the reference level is taken at the bottom of the hill (where the potential energy is zero).
So, we have:
m = 670 kg is the mass of the rock
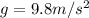
h = 240 m is the initial height of the rock
So, the potential energy of the rock just before the slide is
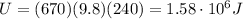
b)
The energy transferred to thermal energy during the slide is equal to the work done by friction, which is:
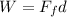
where
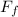 is the force of friction
is the force of friction
d = 740 m is the displacement of the rock along the ramp
The force of friction is given by:
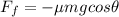
where
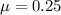 is the coefficient of friction
is the coefficient of friction
m = 670 kg is the mass of the rock
 is the angle of the ramp
is the angle of the ramp
Since we know the lenght of the ramp (d = 740 m) and the height (h = 240 m), we can find the angle:
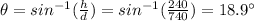
Therefore, the work done by friction is:
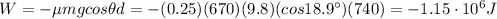
So, the energy transferred to thermal energy is
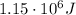 .
.
c)
According to the law of conservation of energy, the kinetic energy of the rock as it reaches the bottom of the hill will be equal to the initial potential energy (at the top) minus the energy transformed into thermal energy.
Therefore, we have:
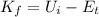
where here we have:
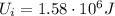 is the potential energy of the rock at the top of the hill
is the potential energy of the rock at the top of the hill
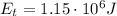 is the energy converted into thermal energy
is the energy converted into thermal energy
Substituting, we find
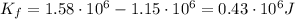
So, this is the kinetic energy of the rock at the bottom of the hill.
d)
The kinetic energy of the rock at the bottom of the hill can be rewritten as
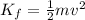
where
m is the mass of the rock
v is its final speed
In this problem, we have:
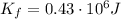 is the final kinetic energy of the hill
is the final kinetic energy of the hill
m = 670 kg is the mass of the rock
Therefore, the final speed of the rock is: