Question

A straight trail with a uniform inclination of 11 degrees from a lodge at an elevation of 700 feet to a mountain lake at an elevation of 8200 feet. What is the length of the trail (to the nearest foot)?

Answer 1

Length of the trail = 39473.68 ft

Explanation:

Let x be the length of the trail.

Given:

Lodge Elevation = 700 ft

Mountain elevation = 8200 ft

Inclination of trail = 11°

We need to find the length of the trail.

Solution:

Total ascent is difference between mountain elevation and lodge elevation.

`Total\ ascent = Mountain\ elevation-lodge\ elevation`

`Total\ ascent = 8200-700`

`Total\ ascent = 7500\ ft`

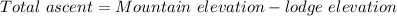
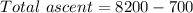
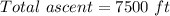
Length of the trail is the length of the hypotenuse of right angle triangle where the length of the shortest side is the right angle triangle is 7500 ft and opposite angle is 11°.

Using cosine rule.

`sin(a) = (Shortest\ side)/(hypotenuse)`

`sin(11) = (7500)/(x)`

`x = (7500)/(sin(11))`

`x = (7500)/(0.19)`

`x = 39473.68\ ft`

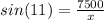
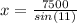
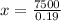
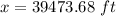
Therefore, the length of the trail is equal to 39473.68 ft.