Answer:
The x-coordinate of R' is 7
Explanation:
we have

This is the equation of a vertical parabola, open upward
The vertex is the point (0,0)
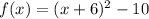
This is the equation of a vertical parabola, open upward
The vertex is the point (-6,-10)
so
The transformation of
p(x) -----> f(x)
(0,0) -----> (-6,-10)
The rule of the transformation is
(x,y) -----> (x-6,y-10)
That means ----> The translation is 6 units at left and 10 units down
Applying the rule of the translation to point R
R(13, 169) ------> R'(13-6, 169-10)
R(13, 169) ------> R'(7, 159)
therefore
The x-coordinate of R' is 7