Answer: Reflection across the x-axis.
Explanation:
The correct exercise is: The correct exercise is: "If the parent function
 is transformed to
is transformed to
 , which type of transformation occurs?
, which type of transformation occurs?
"
There are several transformations for a function f(x). Two of those transformations are shown below:
1. If
 , then the function is reflected across the x-axis.
, then the function is reflected across the x-axis.
2. If
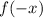 , then the function is reflected across the y-axis.
, then the function is reflected across the y-axis.
In this case, the exercise provides you the following function f(x):

And you know that the function g(x) is obtained by transforming the function f(x). The function g(x) is:

Which can written as:
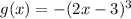
Therefore, you can identify (based on the transformations shown at the beginning of the explanation), that:
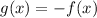
Therefore, the function
 is obtained by reflecting the function
is obtained by reflecting the function
 across the x-axis.
across the x-axis.