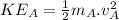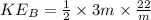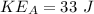Question

Particle A and particle B are held together with a compressed spring between them. When they are released, the spring pushes them apart, and they then fly off in opposite directions, free of the spring. The mass of A is 3.00 times the mass of B, and the energy stored in the spring was 132 J. Assume that the spring has negligible mass and that all its stored energy is transferred to the particles. Once that transfer is complete, what are the kinetic energies of each particle A and B in Joules?

Answer 1

`KE_A=33\ J`

`KE_B=99\ J`

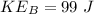
Step-by-step explanation:

Given:

Let mass of the particle B be,
`m_B=m`

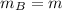
then the mass of particle A,
`m_A=3m`

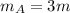
Energy stored in the compressed spring,
`E=132\ J`

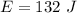
Now when the compression of the particles with the spring is released, the spring potential energy must get converted into the kinetic energy of the particles and their momentum must be conserved.

Kinetic energy:

`(1)/(2)m_A.v_A^2+(1)/(2)m_B.v_B^2=132`

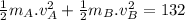
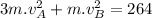`3m.v_A^2+m.v_B^2=264` .............................(1)

Using the conservation of linear momentum:

`m_A.v_A+m_B.v_B=0`

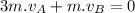`3m.v_A+m.v_B=0` .............................(2)

Put the value of
`v_A` from eq. (2) into eq. (1)

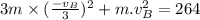
`3m* ((-v_B)/(3))^2+m.v_B^2=264`

`v_B^2=(198)/(m)` ...........................(3)

Now the kinetic energy of particle B:

`KE_B=(1)/(2)* m_B* v_B^2`

`KE_B=(1)/(2)* m* (198)/(m)`

`KE_B=99\ J`

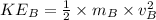
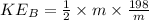
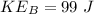
Put the value of
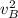`v_B^2` form eq. (3) into eq. (1):

`v_A^2=(22)/(m)`

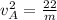
Now the kinetic energy of particle A:

`KE_A=(1)/(2)m_A.v_A^2`

`KE_B=(1)/(2)* 3m* (22)/(m)`

`KE_A=33\ J`