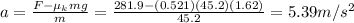Question

A crate of 45.2-kg tools rests on a horizontal floor. You exert a gradually increasing horizontal push on it and observe that the crate just begins to move when your force exceeds 310N . After that you must reduce your push to 231N to keep it moving at a steady 25.2cm/s .

Part A: What is the coefficient of static friction between the crate and the floor?
Part B: What is the coefficient of kinetic friction between the crate and the floor?
Part C: What push must you exert to give it an acceleration of 1.13m/s^2 ? (in N)Part D: Suppose you were performing the same experiment on this crate but were doing it on the moon instead, where the acceleration due to gravity is 1.62 m/s^2. What magnitude push would cause it to move? (in N)
Part E: What would its acceleration be if you maintained the push in part C?

Answer 1

A) 0.700

B) 0.521

C) 281.9 N

D) 51.3 N

E)
`5.39 m/s^2`

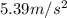
Step-by-step explanation:

A)

In this problem, we apply more and more horizontal push until the crate starts moving.

This occurs when the force exceeds the value of 310 N. This means that the maximum force of static friction between the crate and the floor is equal to 310 N.

The maximum force of static friction can be written as (for an object on an horizontal floor)

`F_s=\mu_s mg`

where

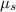`\mu_s` is the coefficient of static friction

m is the mass of the crate

`g=9.8 m/s^2` is the acceleration due to gravity

Here we have:

m = 45.2 kg

`F_s=310 N`

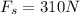
Therefore, the coefficient of static friction is

`\mu_s=(F_s)/(mg)=(310)/((45.2)(9.8))=0.700`

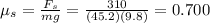
B)

After the crate starts to move, now there is the force of kinetic friction acting on it.

When the crate is moving, its velocity is constant: this means that its acceleration is zero, so according to Newton's second law, the net force on it is zero:

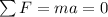`\sum F=ma=0` (1)

The net force (in the horizontal direction) is given by two forces:

- The forward push, F = 231 N

- The force of kinetic friction,
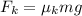`F_k=\mu_k mg`, in the backward direction

So we can rewrite (1) as

`F-\mu_k mg=0`

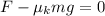
where
`\mu_k` is the coefficient of kinetic friction.

Re-arranging the equation, we can find
`\mu_k`:

`\mu_k=(F)/(mg)=(231)/((45.2)(9.8))=0.521`

C)

In this case, the crate is accelerating at a rate of

`a=1.13 m/s^2`

Therefore we can rewrite Newton's second law as

`\sum F=F-\mu_k mg = ma`

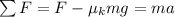
where

F is the push that must be applied

`\mu_k=0.521` is the coefficient of kinetic friction

m = 45.2 kg is the mass

`g=9.8 m/s^2` is the acceleration due to gravity

`a=1.13 m/s^2` is the acceleration

Solving for F, we find:

`F=ma+\mu_k mg=(45.2)(1.13)+(0.521)(45.2)(9.8)=281.9 N`

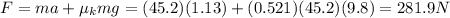
D)

In this case, we are on the Moon, so the acceleration due to gravity is

`g=1.62 m/s^2`

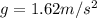
The maximum force of static friction on the crate on the Moon would be therefore:

`F_s=\mu_s mg`

where

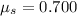`\mu_s=0.700` is the coefficient of static friction (assuming the floor remains of the same material)

m = 45.2 kg is the mass of the crate

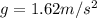`g=1.62 m/s^2` is the acceleration due to gravity

Substituting, we find:

`F_s=(0.700)(45.2)(1.62)=51.3 N`

Therefore, this is the minimum push that must be applied in order to move the crate.

F)

Newton's second law of motion in this situation is:

`F-\mu_k mg = ma`

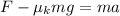
where:

F = 281.9 N is the push applied on the crate (the same as part C)

`\mu_k=0.521` is the coefficient of kinetic friction

m = 45.2 kg is the mass of the crate

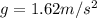`g=1.62 m/s^2` is the acceleration due to gravity

a is the new acceleration

Solving for a, we find the acceleration that the crate would have on the Moon:

`a=(F-\mu_k mg)/(m)=(281.9-(0.521)(45.2)(1.62))/(45.2)=5.39 m/s^2`