Question

Find the area Of each figure. Round to the nearest tenth.

Answer 1

The volume of the cone is 104.7 cubic feet. The volume of the half-sphere is 261.8 cubic feet and the area of the entire figure is 366.5 cubic feet.

Explanation:

Step 1:

The figure consists of a cone and a half-sphere on top. We will have to calculate the volumes of the cone and the half-sphere separately and then add them to obtain the total volume.

Step 2:

The volume of a cone is determined by multiplying
`(1)/(3)` with π, the square of the radius (r²) and height (h).

The radius is 5 feet and the height is 4 feet.

The volume of the cone =
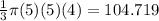`(1)/(3) \pi (5) (5) (4) = 104.719` cubic feet. Rounding this off, we get 104.7 cubic feet.

Step 3:

The area of a half-sphere is half of a full sphere.

The volume of a sphere is given by multiplying
`(4)/(3)` with π and the cube of the radius (r³).

Here the radius is 5 feet.

The volume of a full sphere
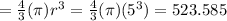`= (4)/(3) (\pi) r^(3) = (4)/(3) (\pi)(5^(3) ) = 523.585` cubic feet.

Step 4:

The volume of the half-sphere =
`(fullspherevolume)/(2) = (523.585)/(2) =261.792.`

The volume of the half-sphere is 261.792 cubic feet. Rounding this off, we get 261.8 cubic feet.

Step 5:

The total volume = The cone's volume + The half sphere's volume,

The total volume
`= 104.719 + 261.792 = 366.511` cubic feet. By rounding this off to the nearest tenth we get 366.5 cubic feet.