Question

If 6 smarties and 5 jujubes cost 40 cents while 3 smarties and 2 jujubes cost 19 cents - how much are each on separately.

Answer 1

Cost of each smarties is 5 cents and cost of each jujubes is 2 cents.

Solution:

Let x be the smarties and y be the jujubes.

Cost of 6 smarties and 5 jujubes = 40 cents

⇒ 6x + 5y = 40 ---------- (1)

Cost of 3 smarties and 2 jujubes = 19 cents

⇒ 3x + 2y = 19 ---------- (2)

Subtract 3x on both sides.

⇒ 2y = 19 – 3x

Divide by 2 on both sides.

`$\Rightarrow y=(19-3x)/(2)` ---------- (3)

Substitute this in equation (1), we get

`$6x+5\left((19-3x)/(2)\right)=40`

`$6x+\left((95-15x)/(2)\right)=40`

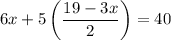
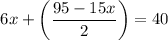
Multiply 6x by
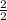`(2)/(2)`, we get

`$(12x)/(2) +(95-15x)/(2)=40`

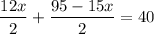
Multiply by 2 on both sides, we get

12x + 95 – 15x = 80

–3x + 95 = 80

Subtract 95 from both sides, we get

–3x = –15

Divide by –3 on both sides,

x = 5

Substitute x = 5 in equation (3)

`$\Rightarrow y=(19-3(5))/(2)`

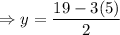
⇒ y = 2

Hence cost of each smarties is 5 cents and cost of each jujubes is 2 cents.