Answer:
Minimum number of photons required is 1.35 x 10⁵
Step-by-step explanation:
Given:
Wavelength of the light, λ = 850 nm = 850 x 10⁻⁹ m
Energy of one photon is given by the relation :
 ....(1)
....(1)
Here h is Planck's constant and c is speed of light.
Let N be the minimum number of photons needed for triggering receptor.
Minimum energy required for triggering receptor, E₁ = 3.15 x 10⁻¹⁴ J
According to the problem, energy of N number of photons is equal to the energy required for triggering, that is,
E₁ = N x E
Put equation (1) in the above equation.

Substitute 3.15 x 10⁻¹⁴ J for E₁, 850 x 10⁻⁹ m for λ, 6.6 x 10⁻³⁴ J s for h and 3 x 10⁸ m/s for c in the above equation.
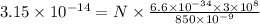
N = 1.35 x 10⁵