Question

Fifty-three percent of U.S households have a personal computer. In a random sample of 250 households, what is the probability that fewer than 120 have a PC?

Answer 1

The correct Answer is 0.0571

Step-by-step explanation:

53% of U.S. households have a PCs.

So, P(Having personal computer) = p = 0.53

Sample size(n) = 250

np(1-p) = 250 * 0.53 * (1 - 0.53) = 62.275 > 10

So, we can just estimate binomial distribution to normal distribution

Mean of proportion(p) = 0.53

Standard error of proportion(SE) =
`\sqrt{(p(1-p))/(n) }` =
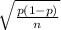`\sqrt{(0.53(1-0.53))/(250) }` = 0.0316

For x = 120, sample proportion(p) =
`(x)/(n)` =
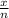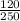`(120)/(250)` = 0.48

So, likelihood that fewer than 120 have a PC

= P(x < 120)

= P( p^​ < 0.48 )

= P(z <
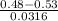`(0.48-0.53)/(0.0316)`​) (z=
`(p^-p)/(SE)`​)

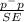= P(z < -1.58)

= 0.0571 ( From normal table )