Question

A wheel rotating with a constant angular acceleration turns through 18 revolutions during a 6 s time interval. Its angular velocity at the end of this interval is 12 rad/s. What is the angular acceleration of the wheel? Note that the initial angular velocity is not zero. Answer in units of rad/s 2 .

Answer 1

The angular acceleration is 1.825 rad/s²

Step-by-step explanation:

Given that,

Angular velocity = 12 rad/s

Number of revolution = 18

Time = 6 sec

The wheel rotates during the 6 s interval is

`\theta=18*2\pi`

`\theta=36\pi\ rad`

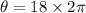
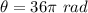
We need to calculate the angular acceleration

Using formula of displacement

`\theta=(1)/(2)*(\omega_(i)+\omega_(f))* t`

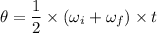
Put the value into the formula

`36\pi=(1)/(2)*(\omega_(i)+12)*6`

`\omega_(i)=(\pi)/(3)`

`\omega_(i)=1.047\ rad/sec`

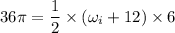
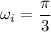
We need to calculate the angular acceleration

Using formula of angular acceleration

`\alpha=(\omega_(f)-\omega_(i))/(t)`

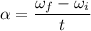
Put the value into the formula

`\alpha=(12-1.047)/(6)`

`\alpha=1.825\ rad/s^2`

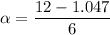
Hence, The angular acceleration is 1.825 rad/s²