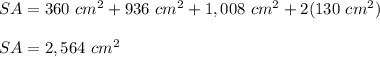Question

What is the surface area of the given figure?

Answer 1

Answer:
`SA=2,564\ cm^2`

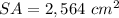
Explanation:

The area of a rectangle can be calculated with this formula:

`A=lw`

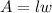
Where "l" is the length and "w" is the width.

The area of a triangle can be found using the following formula:

`A=(bh)/(2)`

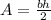
Where "b" is the base of the triangle and "h" is the height.

You can observe that the figure is formed by three different rectangles, Using the formulas, you ge that the area of each rectangle is:

`A_1=(10\ cm)(36\ cm)=360\ cm^2\\\\A_2=(36\ cm)(26\ cm)=936\ cm^2\\\\A_3=(36\ cm)(28\ cm)=360\ cm^2=1,008\ cm^2`

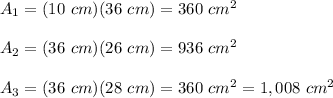
The triangles are equal, then, using the formula shown above, you get that the area of each of them is:

`A_4=A_5=((26\ cm)(10\ cm))/(2)=130\ cm^2`

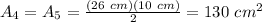
Adding all the areas, you get that the surface area of the figure is:

`SA=360\ cm^2+936\ cm^2+1,008\ cm^2+2(130\ cm^2)\\\\SA=2,564\ cm^2`