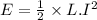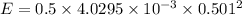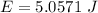Answer:
a)
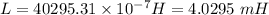
b)
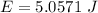
Step-by-step explanation:
Given:
- no. of turns in the solenoid,
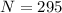
- radius of the solenoid,
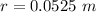
- length of the solenoid,
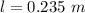
a)
The inductance of the solenoid is given as:
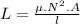
where:
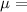 permeability of the free space
permeability of the free space
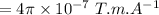
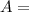 cross sectional area of coil formed
cross sectional area of coil formed
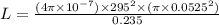
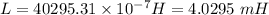
b)
current in the coil,
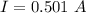
The energy stored in the solenoid can be given as: