Question

The electric cooperative needs to know the mean household usage of electricity by its non-commercial customers in kWh per day. Assume that the population standard deviation is 2.4 kWh. The mean electricity usage per family was found to be 17.5 kWh per day for a sample of 796 families. Construct the 90% confidence interval for the mean usage of electricity. Round your answers to one decimal place.

Answer 1

The 90% confidence interval for the mean usage of electricity is between 17.4 kwH and 17.6 kwH

Explanation:

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1-0.9)/(2) = 0.025`

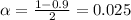
Now, we have to find z in the Ztable as such z has a pvalue of
`1-\alpha`

So it is z with a pvalue of 1-0.05 = 0.95, so z = 1.645

Now, find the margin of error M as such

`M = z*(\sigma)/(√(n))`

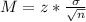
In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

So

`M = 1.645*(2.4)/(√(796)) = 0.14`

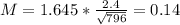
The lower end of the interval is the mean subtracted by M. So 17.5 - 0.14 = 17.4 kwH

The upper end of the interval is M added to the mean. So 17.5 + 0.14 = 17.6 kwH

The 90% confidence interval for the mean usage of electricity is between 17.4 kwH and 17.6 kwH