Question

Two brothers want to share a large field equally.

One brother proposes to take all the regions labeled A.

Answer 1

Yes, the partition gives the two brothers equal shares.

Explanation:

Step 1:

Assume the entire field has an area of B. So one brother takes
`(1)/(12) B`,
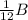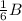`(1)/(6)B`, and
`(1)/(4) B`

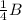
So we need to calculate how much this brother takes in terms of B.

To do this we calculate how much
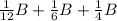`(1)/(12) B + (1)/(6) B + (1)/(4) B` is.

Step 2:

To add
`(1)/(12) B + (1)/(6) B + (1)/(4) B`,

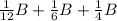First take the LCM of the denominators 12, 6, and 4

The LCM is 12, we multiply the denominator to get the LCM value, this same value is multiplied to the numerator too.

`(1)/(12) B + (1)/(6) B + (1)/(4) B = (1(1))/(12(1)) B + (1(2))/(6(2)) B + (1(3))/(4(3)) B \\\\(1)/(12) B + (1)/(6) B + (1)/(4) B= (1B +2B+3B)/(12) = (B)/(2)`

Step 3:

One brother gets
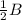`(1)/(2) B`, so we need to calculate how much the other brother gets.

The other brother's share =
`B - (1)/(2) B = (1)/(2)B`

So both the brothers get equal shares