Answer:
The probability that it takes more than 30 lines of code until Joe finds his first bug is 0.2821.
Explanation:
Let X = number of bugs in every 25 lines of code.
The probability of the random variable X is,
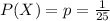 .
.
The random variable X follows a Geometric distribution.
A Geometric distribution is the probability distribution of the number of Bernoulli trials needed before the first success.
The probability mass function of Geometric distribution is:
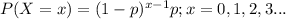
Compute the probability that it takes more than 30 lines of code until Joe finds his first bug as follows:
P (X > 30) = 1 - P (X ≤ 30)
![=1-\sum\limits^(30)_(x=0)[(1-(1)/(25))^(x-1)(1)/(25)]\\=1-0.7179\\=0.2821](https://img.qammunity.org/2021/formulas/mathematics/college/u9ubzljca2ku4t1jwlnd3vvsavgasww7us.png)
Thus, the probability that it takes more than 30 lines of code until Joe finds his first bug is 0.2821.